Simulating the swelling and deformation behaviour in soft tissues using a convective thermal analogy

Abstract

Background

It is generally accepted that cartilage adaptation and degeneration are mechanically mediated. Investigating the swelling behaviour of cartilage is important because the stress and strain state of cartilage is associated with the swelling and deformation behaviour. It is well accepted that the swelling of soft tissues is associated with mechanical, chemical, and electrical events.

Method

The purpose of the present study was to implement the triphasic theory into a commercial finite element tool (ABAQUS) to solve practical problems in cartilage mechanics. Because of the mathematical identity between thermal and mass diffusion processes, the triphasic model was transferred into a convective thermal diffusion process in the commercial finite element software. The problem was solved using an iterative procedure.

Results

The proposed approach was validated using the one-dimensional numerical solutions and the experimental results of confined compression of articular cartilage described in the literature. The time-history of the force response of a cartilage specimen in confined compression, which was subjected to swelling caused by a sudden change of saline concentration, was predicted using the proposed approach and compared with the published experimental data.

Conclusion

The advantage of the proposed thermal analogy technique over previous studies is that it accounts for the convective diffusion of ion concentrations and the Donnan osmotic pressure in the interstitial fluid.

Background

The extracellular matrix (ECM) of articular cartilage is negatively charged and hydrated [1, 2]. Under normal physiological conditions, the fixed negative charge in ECM is electrically neutralized by mobile cations and anions contained in the synovial fluid. The difference in ion concentration between the ECM and synovial fluid introduces a fluid pressure difference between them, the so-called Donnan osmotic pressure [3]. At equilibrium, the swelling pressure, which consists of the Donnan osmotic pressure and a charge-to-charge expansion stress within the tissue, is counteracted by structural elements in the solid matrix.

It is well accepted that the swelling of soft tissues is associated with mechanical, chemical, and electrical events. The triphasic theory [4], which was generalized by Gu et al. [5] to include multiple ion species, is the only realistic model currently available to describe the mechanics of articular cartilage swelling. Gu et al. [6] and Gu [7] used the triphasic theory to analyse the coupling between fluid and ion transport, streaming potential, and deformation of cartilage during compression tests. Bryant and McDonnell [8] applied the triphasic theory to analyse corneal swelling under steady-state conditions in which the effects of fluid flow were neglected. Recently, Hon et al. [9] developed a rigorous numerical algorithm of the triphasic model for two-dimensional problems based on radial basis functions. However, all numerical/analytical approaches mentioned above are problem-oriented, and cannot be used for solving realistic biological problems, which are usually nonlinear, three-dimensional, irregular and complex in geometry, and undergo large deformations.

In order to apply the triphasic theory to biological systems, or applied biomechanical problems, the triphasic constitutive equations must be implemented into a finite element model (FEM). Simon et al. [10] proposed a poroelastic finite element formulation that included transport and swelling effects in soft tissue. This model might be considered a special case of the triphasic model by Lai et al. [4]. Simon et al. [10] developed a one-dimensional FEM that was used to demonstrate the properties of triphasic materials. However, it could not be used for practical problems in two- or three-dimensional space. Sun et al. [11] developed sophisticated FEM formulations that included the coupling between mechanical, electrical and chemical events in articular cartilage. However, the approach proposed by [11] still in a conceptual stage and needs substantial research and development until it can be used for solving realistic biological problems.

Because the process of diffusion is mathematically equivalent to the process of thermal transfer, the transport of ions in cartilage may be analysed using a thermal analogy. Myers et al. [12] simulated swelling of articular cartilage using a thermal analogous technique. Kaufmann et al. [13] analysed poroelastic problems with swelling deformation using a commercially available FEM software package (ABAQUS). In these last two studies, the diffusion process of ion concentrations was analysed by neglecting convection, i.e., by assuming that the velocity of the tissue and the diffusion of ions are decoupled. For most substances, the diffusion process is strongly coupled with the velocity of the media. Therefore, the coupling between the velocity of the tissue and the diffusion of ions may have non-negligible effects in physiological problems.

Understanding the mechanisms of swelling and deformation is important when investigating the mechanics and adaptative behaviour of articular cartilage. The triphasic theory [4, 5] can be used to describe swelling and transport of ions in articular cartilage. However, a commercial finite element tool based on the triphasic theory, which bioengineers can use to analyse swelling and deformation behaviour for real-life biophysical problems, does not exist. The purpose of this study was to implement the triphasic theory [4, 5] into a commercially available finite element software package (ABAQUS), and to validate the proposed approach using the one-dimensional numerical solutions by Simon et al. [10], and the experimental results of confined articular cartilage compression obtained by Eisenberg and Grodzinsky [14]. In order to solve the problem using ABAQUS, the triphasic model was converted into a thermo-mechanical interaction problem with convective heat transfer. It was assumed that the volume occupied by ions is small and that the effect of electric current on the flow of ions can be ignored.

Method

Governing Equations

Articular cartilage was assumed to obey the triphasic model proposed by Lai et al. [4] and Gu et al. [5]. For infinitesimal deformation, the constitutive equation is expressed as

where I is the unit tensor; σ^s, σ^f, and σ^trepresent the stresses in the solid phase, in the interstitial fluid, and in the total tissue; λ and μ are the first and the second Lamé constants; p and ε are fluid pressure and strain of the solid phase, respectively. The stress in the solid phase (σ^s) is decomposed here into three parts: a component associated with the fluid pressure (-Φ^s p I), a chemical expansion stress (T _c I), and an elastic stress associated with the deformation of the matrix. Φ^sand Φ^fare the solid and fluid volume fractions, respectively. Assuming that the volumetric fraction of ions, Φ^- and Φ⁺, is negligible, as suggested by Gu et al. [5] and Sun et al. [11], one can write the equation of the mixture in the form:

Φ^s+ Φ^f+ Φ^- + Φ⁺ ≈ Φ^s+ Φ^f= 1     (2)

The ECM is negatively charged, with a fixed charge density of c^F. Everywhere within the tissue under physiological conditions, the electroneutrality condition is maintained by

c⁺ = c^- + c^F    (3)

where c⁺ and c^- are concentrations of mobile cations and anions, respectively. c⁺, c^-, and c^Fare measured in moles per unit fluid volume.

The conservation of momentum is satisfied everywhere in the tissue

where υ^sand υ^fare the velocities of solid and fluid, k is the hydraulic permeability (open circuit). The continuity condition holds everywhere in the tissue, such that

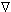
.(Φ^fυf+ Φ^sυs+ Φ^- υ^- + Φ⁺ υ⁺) = 0     (5)

Darcy's law is obtained from the second equation of the conservation of momentum (4).

W _i = Φ^f(υ^f- υ^s) = -k 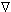p     (6)

where W _i is the effective fluid flux.

Fluid pressure p is composed of hydrostatic pressure, p ₀; and osmotic pressure [15], Δπ:

p = p ₀ - Δπ     (7)

The osmotic pressure is associated with the chemical potential and is expressed explicitly

π = ξRT [c + A ₀ c² + A ₁ c³ + ··· ];

Δπ = π - π₀     (8)

where π₀ is the initial state of the system; ξ is the osmotic coefficient describing the character of the ion transport through the semi-permeable membrane (tissue). ξ approaches 1 for an ideal membrane, i.e., no ions can pass through the tissue. R and T are the gas constant and absolute temperature, respectively. c is the effective NaCl concentration within the tissue which is related to the concentration of c^- and c⁺ by [14]:

In a first order approximation, Eq. (8) takes the form of van't Hoff's equation:

π = ξR·T·c;

Δπ = π - π₀.     (10)

The dependence of the chemical expansion stress, T _c , on the ion concentration has not been quantified based on a strict theory. Eisenberg and Grodzinsky [14] proposed a chemical expansion stress as a function of c

where β₀ and c _β are material parameters.

Another form of T _c as a function of c^- and c^Fwas proposed by Lai et al. [4]

where a ₀ and κ are material parameters; γ and γ* are the activity coefficients of NaCl in the tissue and the external solution, respectively.

Conservation of mass requires

where ρ^α is the the apparent density for component α; the superscripts α = s, f, +, - represent the solid and fluid phase, and cations and anions, respectively; t is time.

Using the relations [4] ρ^α = c^α M^α (α = +, -) with M⁺ and M^- being the atomic weight of Na⁺ and Cl^-, respectively, Eq.(13) can be written for electrolytes as

The diffusion of the electrolytes can be described using Fick's law

• D^α 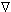c^α = c^α (υ^α - υ^s) α = -, +     (15)

where D^α is the diffusion coefficient for component α.

Fick's diffusion law (15), combined with mass conservation (Eq.(14)), results in the governing equation of the convective diffusion process

where the effects of the volume strain rate of the solid phase on the diffusion process have been neglected. The diffusion problem (Eq. (16)) can be solved using a convective, thermal analogy, i.e., c^α → θ with θ denoting temperature.

The equations of motion for fluid and electrolytes (c⁺ and c^-) in the triphasic model of Lai et al. [4] [their Eqs. (30–32)] are reduced to Darcy's law (Eq. (6)) and Fick's law (Eq. (15)) when the effects of the electrical potential, the friction between ions and fluid, the friction between ions and anions, and the effects of the volumetric deformation rate of the solid phase on the fluid phase are neglected.

Solution Procedure

For a practical problem with three components, only c^- needs to be solved, because c⁺ can be obtained from Eq. (3). In order to solve the triphasic problem, the triphasic constitutive relation (1) was converted into a biphasic equation [2] with thermal expansion,

ε = ε^e+ ε^c= ε^e+ K Δc I    (17)

where ε is the total tissue strain, ε^eis the elastic strain associated with mechanical loading, and ε^cis the strain associated with the chemical expansion stress ("thermal strain"); K = K(c) is a "thermal expansion coefficient", defined as

where E is the Young's modulus of the tissue.

Eq. (17) is in a form that can be implemented into a general, commercial software package. A practical problem can now be solved using an iterative technique as follows:

• (a) The initial c distribution within the tissue is obtained by solving the diffusion equation (16) using υ^s= 0. The problem is equivalent to the diffusion of c through the tissue in a steady-state. The boundary condition, i.e., the distribution of c on the surface of the tissue, is known.

• (b) The triphasic problem [Eqs. (1)] is solved using the distribution of c in the tissue obtained in the previous step. The problem is solved using a thermal analogous procedure, as discussed previously. From this step, the distributions of the stress/strain and the displacement rate of the solid phase (υ^s) were obtained.

• (c) The diffusion equation (16) is solved again using the updated υ^sobtained in the previous step. This is realized using a convective thermal analogous procedure, as discussed previously.

The iterations [steps (b) and (c)] are continued until the problem has converged. The distributions of the stress/strain and the displacement rate of the solid phase (υ^s) were extracted from the simulation results via a customized subroutine, and the iterations were run manually. In the present simulations, the effective salt concentration in the bath is assumed to be constant.

Numerical Tests

In order to validate the proposed FEM approach, our results were compared to those obtained by Simon et al. [10] and Eisenberg and Grodzinsky [14]. All simulations were performed using a confined compression configuration (Fig. 1). The tissue specimens were compressed in a confining chamber with a rigid, porous platen connected to a load cell. The concentration of NaCl in the bathing solution, (c(t)), and the compression displacement of the sample, (δ(t)), were prescribed, while the compression force (F(t)) was predicted in all simulations. ABAQUS (version 5.8) was used in all simulations [16]. In the analysis, thermal expansion of the fluid was neglected. All numerical simulations were carried out using 8-node, biquadratic, axi-symmetric elements. The distribution of NaCl concentration within the bathing solution was considered to be uniform throughout the tests.

Figure 1

Schematics of the numerical tests simulating the confined compression experiments by Eisenberg and Grodzinsky [14]. The cartilage specimen was compressed in a rigid, impermeable chamber. The displacement δ(t) and the NaCl concentration of the bathing solution c(t) were controlled, while the reaction force, F(t), was measured in the physical experiments [14] or was predicted in the numerical tests.

Numerical Test A was designed to reproduce the one-dimensional, finite element results by Simon et al. [10]. The cartilage specimen had a thickness of 5.0 mm and a diameter of 30.0 mm. The specimen was compressed using a prescribed displacement and, at the same time, the ion concentration at the surface of the specimen was changed. The c^- concentration was chosen as the reference parameter in the simulations. At t = 0, the specimen was in a strainless equilibrium condition and had an original, uniform c^- concentration of 0.001 M. The specimen was compressed via a prescribed step function (Fig. 2a); the c^- concentration on the surface of the specimen was increased suddenly and then kept constant (Fig. 2b) for the remainder of the test. All material parameters (D, k, H _A , and v) were assumed to be constant (Tables 1, 2, 3).

Figure 2

Displacement and c^- concentration at the central line of the specimen as a function of time for TEST A: (a) displacements at the bottom (z = 0.0, prescribed) and at the center of the specimen (z = 0.5 h, predicted) as a function of time; (b) c^- concentrations at different locations within the specimen as a function of time. The concentration at the surface of the specimen was prescribed, while the concentration within the specimen was predicted using the present model. The setup for the numerical test is shown in Fig. 1, with d = 32.0 mm and h = 5.00 mm. The material properties used are listed in Table 1 (TEST A).

Table 1 Geometry and Constant Material Parameters used in the Simulations. These parameters were taken from the literature [14, 10]

Table 2 Aggregate Modulus used in the Simulations. A constant aggregate modulus was used for Test A [10]. A NaCl concentration-dependent aggregate modulus was used for Tests B and C [14]

Table 3 Parameters for the Chemical Expansion Stress used in the Simulations. The parameters of the chemical expansion stress [i.e., Eq. (12)] for Test A were from Lai et al. [4] and Gu et al. [5]. The parameters for the chemical expansion stress [i.e., Eq. (11)] for Tests B and C were from Eisenberg and Grodzinsky [14]

Numerical Tests B and C were designed to reproduce the confined compression experiments by Eisenberg and Grodzinsky [14]. The articular cartilage specimens had a diameter of 6.40 mm, and had an original thickness of 0.540 mm and 0.565 mm for Tests B and C, respectively. The specimens were compressed initially by an amount of δ₀ = 0.0560 mm and 0.0185 mm for Tests B and C, respectively. The initial NaCl concentrations in the bathing solution were c* = 0.10 and 0.005 M for Tests B and C, respectively. The specimen was kept in this state for 2000 seconds until the predicted force reached a steady-state (F ₀ = 2.31 N and 2.28 N for Tests B and C, respectively). Once the steady-state force had been reached, the NaCl concentration was changed suddenly from the initial value (c*) to 0.15 M and 0.10 M, for tests B and C, respectively, while the compression of the specimen was kept constant. The predicted and the measured [14] forces were normalized to the steady-state force F ₀, and were plotted as a function of time. The aggregate modulus, H _A , was assumed to be linearly dependent on c. Other parameters (D, k, and v) were assumed to be constant (Tables 1, 2, 3) [14].

Van't Hoff's equation [Eq. (10)] was used in all simulations to evaluate the osmotic pressure.

Results

The numerical results of Test A are illustrated in Figs. 2 and 3. The predicted displacement at the center of the specimen and the c^- concentration at different locations across the thickness of the specimen as a function of time are shown in Fig. 2a and 2b, respectively. c^- concentration distributions across the thickness of the articular cartilage specimen as a function of time are shown in Fig. 3. In order to compare our three-dimensional (axi-symmetrical) simulation to the one-dimensional FEM simulation by Simon et al. [10], only the results on the central line of the specimen were used in these plots. The numerical results of Simon et al. [10] are also shown in these figures.

Figure 3

The predicted c^- concentration distributions across the thickness of the specimen (at the central line) as a function of time for TEST A. The setup for the numerical test is shown in Fig. 1, with d = 32.0 mm and h = 5.00 mm. The material properties used are listed in Table 1 (TEST A).

The numerical results of Tests B are shown in Fig. 4. The time-histories of the c^- concentration prescribed on the top of the specimen (z/h = 1), together with those predicted at a depth of z/h = 1/8 and 7/8 on the central line of the specimen, are shown in Fig. 4a. The prescribed displacement at the top of the specimen as a function of time is depicted in Fig. 4b. The predicted specimen reaction force as a function of time, in response to the variations in salt concentration and displacement, are shown in Fig. 4c. Approximately 2000 s after the specimen was exposed to 0.10 M NaCl in the bathing solution and was compressed to δ₀ = 0.056 mm, an equilibrium state (F ₀ = 2.31 N) was reached (Fig. 4c).

Figure 4

NaCl concentration at the central line of the specimen, the compression displacement (δ(t)), and the reaction force, F(t), as a function of time for TEST B. (a) NaCl concentration at the central line and at three different locations (z/h = 1, 1/4, and 7/8) within the specimen as a function of time. The concentration at the surface of the specimen (z = h) as a function of time was prescribed throughout the test. (b) The prescribed compression displacement, δ(t), as a function of time. (c) The predicted reaction force as a function of time, F(t). The reaction force reached a steady-state value (F ₀) within 2000 s. The setup for the numerical test is shown in Fig. 1, with d = 32.0 mm and h = 5.00 mm. The material properties used are listed in Table 1 (TEST B).

The predicted total reaction force on the specimen as a function of time, normalized to the steady-state force, F ₀, were compared with the experimental measurements by Eisenberg and Grodzinsky [14] in Fig. 5a and 5b, for Tests B and C, respectively. t = 0 (Fig. 5) is the time when the specimens reached equilibrium (Fig. 4c).

Figure 5

The predicted reaction force as a function of time compared with the experimental results by Eisenberg and Grodzinsky [14]. (a) TEST B; (b) TEST C. t = 0 is the moment when the specimen reached a steady-state (i.e., F reached F ₀, as shown in Fig. 4) and the concentration of the bathing solution was increased to a new level (Fig. 4). The reaction force was normalized to its value at the steady-state (F(t)/F ₀). The setup for the numerical test is shown in Fig. 1, with d = 32.0 mm and h = 5.00 mm and 6.00 mm for TESTS B and C, respectively. The material properties used are listed in Table 1 (TESTS B and C).

The interaction between mechanical and chemical stresses and deformations during cartilage deforma-tion was demonstrated in our numerical simulations. For example, a sudden change in the deformation state of the tissue caused a change in ion concentration across the thickness of the cartilage specimen (Fig. 2a and 2b), while a change in NaCl concentration caused to a change in stress within the articular cartilage (Fig. 4a,4b,4c).

Discussion and Conclusion

Experimental animal models have shown that articular cartilage becomes thicker [17, 18], softer [19], and more permeable [20] in the initial stages of osteoarthritis (OA). It is assumed that the adaptation and degeneration of articular cartilage is associated with the stress-strain state of articular cartilage during normal, everyday loading. The stress-strain state of articular cartilage is associated with the swelling and deformation of the cartilage, which is influenced by the changing mechanical and chemical environment. A general FEM tool using the triphasic theory, which bioengineers can use to analyse practical swelling and deformation behaviour for physiologically relevant problems, does not exist. Because of the mathematical identity between thermal and mass diffusion processes [21], it is possible to transfer the triphasic model into a suitable form for implementation into commercial finite element software to simulate the swelling and deformation behaviour of articular cartilage. The main difference between the proposed approach and the triphasic model [4] is that the electrical potential and its influence on the transfer of electrolytes (i.e., NaCl concentration) was neglected in the current analysis. The advantage of the proposed thermal analogous technique over previous studies [12, 13] is, that it accounts for the convective diffusion of NaCl concentrations and the Donnan osmotic pressure in the interstitial fluid.

Our simulations (Test A) (Figs. 2b and 3) on the time-dependent distributions of concentrations on the central line of the specimen agree well with the one-dimensional finite element results obtained by Simon et al. [10]. The displacement at the center of the specimen (z/h = 0.5) showed a sudden change (Fig. 2a) when the prescribed displacement at the specimen surface was changed using a step function (Fig. 2a). This behaviour was not predicted by Simon et al. (their Fig. 3) [10], who gave no explanation why they did not predict this behaviour which should occur when considering the articular cartilage as a continuous material.

In order to reach an initial compression force (F ₀), the cartilage specimen must be compressed long enough for the force to reach a steady-state. It was found that the amount of initial compression to reach a given compression force in our numerical tests was smaller than the corresponding compression in the experiments by Eisenberg and Grodzinsky [14]. This difference in the magnitude of compression between theory and experiment is likely associated with the fact that in real tests, there is space between the lateral surface of the cartilage specimen and the chamber wall; while in our numerical simulations, the lateral boundary of the specimen was assumed to be fixed ideally.

The proposed approach differs from the poroelastic finite element formulation by Simon et al. [10] in that the fluid pressure, which is the sum of the hydrostatic and Donnan osmotic pressure, is governed by Darcy's law; while in the model by Simon et al. [10], the effect of the Donnan osmotic pressure was included into the fluid pressure through a "generalized Darcy's" law [Eq. (12b) in [10]].

Compared to the general triphasic model by Lai et al. [4] and Gu et al. [5], the effects of the electrical potential, the friction between ions and fluid, the friction between cations and anions, and the effects of the volumetric deformation rate of the solid phase on the fluid phase were neglected in the proposed approach. The effects of friction between cations and anions and the volumetric deformation rate of the solid phase on the fluid phase are believed to be negligible [5, 11].

The major difference between the proposed approach and the rigorous formulation by Sun et al.'s [11] is that the friction between ions and fluid was neglected in our model formulation. However, the effects of the friction between ions and fluid are included in the diffusion coefficient (D^α) in our model. Our model represents a reasonable approximation of complex biological systems and the associated problems, since the friction between ions and fluid cannot be measured directly, while the diffusion coefficient, which includes the effects of ions/fluid friction, can be determined experimentally.

In the present simulations, a constant osmotic coefficient, hydraulic permeability, and diffusion coefficient was used. However, in reality, these coefficients are not constant; they change as a function of the deformation state of the matrix, the ion concentration, and the electrical potential [6, 7]. Deformation-and ion concentration-dependent coefficients (osmotic coefficient, hydraulic permeability, and diffusion coefficients) can be incorporated into the proposed approach.

In summary, we have developed an approach that converts the triphasic analysis into a problem of convective thermal diffusion coupled with a poroelastic thermal stress analysis. The proposed approach makes it possible for bioengineers to analyse triphasic physiological systems using commercially available FEM software.